Maharishi Baudhayana: Pythagoras of India
 डॉ. संतोष कुमार तिवारी।
डॉ. संतोष कुमार तिवारी।
पाइथागोरस थ्योरम (Pythagoras theorem) अर्थात पाइथागोरस प्रमेय दुनिया भर में गणित के छात्रों को पढ़ाई जाती है। वास्तुकला (Architecture) में इसका बहुत इस्तेमाल होता है। इसके उपयोग के बिना मिस्र के पिरामिड बनाए नहीं जा सकते थे। ये पिरामिड ईसा से ढाई-तीन हजार वर्ष पूर्व बनाए गए थे। सन् 2018 में साइंस एलर्ट (Science Alert) पत्रिका में एक लेख प्रकाशित हुआ “Stonehenge Builders Used Pythagoras’ Theorem 2,000 Years Before He Was Born” अर्थात पाइथागोरस के जन्म से 2,000 वर्ष पूर्व इंग्लैंड के प्रसिद्ध स्टोनहॅन्ज (Stonehenge) के निर्माण में भी पाइथागोरस प्रमेय का इस्तेमाल हुआ। (https://www.sciencealert.com/pythagoras-triangle-used-construction-stonehenge)। स्टोनहॅन्ज का निर्माण ईसा से दो से तीन हजार वर्ष पूर्व हुआ था।
साइंस एलर्ट के लेख में यह बात हूज न्यूमैन (Hugh Newman) की अंग्रेजी पुस्तक ‘Megalith: Studies in Stone’ के हवाले से कही गई। यह पुस्तक सन् 2018 में प्रकाशित हुई। इस पुस्तक में कहा गया “So it’s little surprise that scholars have seen signs of its use among Babylonian, ancient Chinese, and Vedic Indian cultures”. अर्थात विद्वानों को इस बात में कोई आश्चर्य नहीं है कि पाइथागोरस प्रमेय का प्रयोग उनके जन्म से सैकड़ों साल पहले बैबीलोनिया में, प्राचीन चीन में और भारत की वैदिक सभ्यताओं में हुआ।
यूनानी अर्थात ग्रीक दार्शनिक और गणितज्ञ पाइथागोरस का जन्म ईसा से 570 वर्ष पूर्व हुआ था। तो फिर उसके जन्म से डेढ़-दो हजार वर्ष पूर्व उसकी थ्योरम का इस्तेमाल कैसे हुआ? कहने का मतलब यह है कि पाइथागोरस से पहले भी उस थ्योरम अर्थात प्रमेय के बारे में लोग जानते थे।
दुनिया की सबसे पुरानी भाषाएँ हैं – तमिल और संस्कृत। ये दोनों ईसा से 5000 वर्ष पूर्व से अधिक पुरानी हैं। सभी यूरोपीय भाषाओं का उद्गम संस्कृत से हुआ है। भारतीय गणितज्ञ महर्षि बौधायन (Baudhayana) ने ईसा से लगभग 800 वर्ष पूर्व संस्कृत भाषा में वही फार्मूला दिया था जोकि यूनानी दार्शनिक पाइथागोरस ने लगभग ढाई सौ वर्ष पुन: दोहराया। अब इस लेख में नीचे यह बताने का प्रयास है कि यूनान के पाइथागोरस और संस्कृत के महर्षि बौधायन ने क्या कहा।
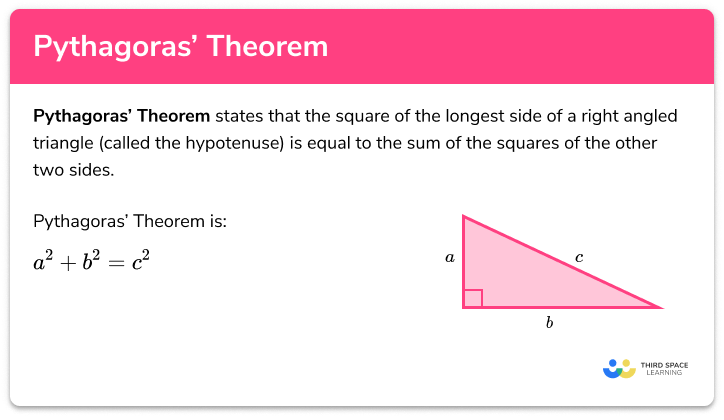
पाइथागोरस थ्योरम अर्थात प्रमेय क्या है?
गणित में पाइथागोरस प्रमेय बहुत ही सामान्य और महत्वपूर्ण विषय है। यह प्रमेय में समकोण त्रिभुज की तीनों भुजाओं के बीच के संबंध की व्याख्या है। समकोण त्रिभुज वह होता है जिसका एक कोण 90 डिग्री का हो। पाइथागोरस प्रमेय से इस त्रिभुज के कर्ण (Hypotenuse) के लम्बाई मालूम की जाती है। पाइथागोरस थ्योरम के अनुसार इस त्रिभुज की अन्य दो भुजाओं के वर्ग को यदि जोड़ दिया जाए और उस योगफल का वर्गमूल निकाला जाए तो वह वर्गमूल ही कर्ण (Hypotenuse) की लंबाई होगी। उदाहरण:
यदि समकोण त्रिभुज की दो भुजाएँ 8 इंच और 6 इंच की हैं, तो उसके कर्ण (Hypotenuse) की लम्बाई पाइथागोरस थ्योरम के अनुसार इस प्रकार होगी:
√ (8×8+6×6) = √ (64+ 36) = √100 =10
मतलब यह है कि उसके कर्ण की लम्बाई 10 इंच होगी।
इसके अतिरिक्त पाइथागोरस का कहना था कि यदि किसी समकोण त्रिभुज की दो भुजाएँ a इंच और b इंच लम्बाई की हैं, तो इन दोनों के वर्गों के क्षेत्रफल को जोड़ने पर हमें कर्ण के वर्ग का क्षेत्रफल के मालूम हो जाएगा। उदाहरण:
यदि यदि समकोण त्रिभुज की दो भुजाएँ 8 इंच और 6 इंच लम्बी हैं, तो इनके वर्गों का क्षेत्रफल जोड़ने पर हमें उसके कर्ण (Hypotenuse) के वर्ग का क्षेत्रफल मालूम हो जाएगा।
(8×8+6×6) = (64+ 36) = 100 वर्ग इंच
पाइथागोरस थ्योरम हर देश और हर काल में सही सिद्ध हुई है।
महर्षि बौधायन का सूत्र
पाइथागोरस का जन्म तो ईसा के जन्म से 570 वर्ष पूर्व हुआ था। जबकि हमारे देश के महर्षि बौधायन का जन्म ईसा से 800 वर्ष पूर्व हुआ था। महर्षि बौधायन जाने-माने गणितज्ञ थे। महर्षि बौधायन का एक सूत्र है:
दीर्घस्याक्षणया रज्जुः पार्श्वमानी तिर्यकं मानी च।
यत्पृथग्भूते कुरुतस्तदुभयांकरोति॥
यदि कर्ण (Hypotenuse) पर कोई रस्सी तानी जाए, तो उस पर बने वर्ग का क्षेत्रफल ऊर्ध्व (Vertical) भुजा पर बने वर्ग तथा क्षैतिज (Horizontal) भुजा पर बने वर्ग के योग के बराबर होता है।
महर्षि बौधायन का यह सूत्र वही है जो लगभग 250 वर्ष बाद यूनान के पाइथागोरस ने भी बताया।
महर्षि बौधायन के निम्नलिखित छह ग्रन्थ हैं:
- बौधायन श्रौतसूत्र
- बौधायन कर्मान्तसूत्र
- बौधायन द्वैधसूत्र
- बौधायन गृह्यसूत्र
- बौधायन धर्मसूत्र
- बौधायन शुल्बसूत्र
इनमें से शुल्बसूत्रों में आरम्भिक गणित और ज्यामिति के बहुत से परिणाम और प्रमेय हैं।
चूँकि संस्कृत और तमिल भाषाएँ दुनिया की सबसे पुरानी भाषाएँ हैं, इसलिए इन भाषाओं में ही योग, गणित, आयुर्वेद, खगोल, भारतीय काल दर्शन, आदि का प्राचीनतम ज्ञान भण्डार भरा हुआ है।
इस लेख के लेखक ने कुछ समय पहले भारत के गणितज्ञ आर्यभट के बारे में एक लेख लिखा था। आर्यभट का जन्म सन् 476 ईस्वी को हुआ था। लेख का शीर्षक था ‘नासा सिद्ध कर रहा है आर्यभट की थ्योरी’। उस लेख को इस URL पर क्लिक करके पढ़ा जा सकता है: https://apkaakhbar.in/nasa-is-proving-aryabhats-theory/
उस समय तक प्राप्त जानकारी के अनुसार लेखक ने उस लेख में लिखा था “वह (आर्यभट) भारत के प्रथम गणितज्ञ और खगोलशास्त्री थे।“ लेकिन बाद किए गए अध्ययन से लेखक को यह पता चला कि आर्यभट से पहले भी महर्षि बौधायन जैसे गणितज्ञ भारत-भूमि पर पैदा हुए थे।
(लेखक सेवानिवृत्त प्रोफेसर हैं।)




